「あみだくじ」でズルされる!?身につけないとヤバい統計リテラシー!本の知識!
知っていますか?
「あみだくじ」には、必勝法があるんです。
統計リテラシーを持つ人たちは知っています。
「“統計”リテラシーなんだから、
『学者や統計家たちは知ってるよ』って話か?」
いいえ、そうとも限りません。
なぜなら、統計リテラシーは、
ビジネスのあらゆる場面で
顔を覗かせるからです。
一流のビジネスマンになるために
統計リテラシーを身につける。
こんなことが普通に考えられるのです。
よって、アドバンテージを持つ
統計リテラシー保持者は
普通に、ゴロゴロいます。
そんな保持者は、「あみだくじ」に始まり、
「データ収集の省力化」や、
「会議時間の削減」など、
統計のパワフルな力を使って、
ズルや楽をしています。
羨ましいですか?
なら、あなたも
こちら側になりましょう!
本『統計学が最強の学問である』が
アナタを導いてくれます。
超簡単に話すので安心してください。
意外と簡単なんですよ?
それでは、行きましょう!
本書の知識を切り抜き、紹介します。
- 「あみだくじ」には、「あたり/はずれ」が、中央にあるのか、端にあるのか、知っていさえすれば勝てる!
- その全数調査、必要ありますか?サンプリング調査でも”妥当な”結果は出せる!
- 予想がつかないなら、さっさと「A/Bテスト」!
- 一つに絞れないなら、さっさと「A/Bテスト」!
- ほとんどのデータが「重回帰分析」か「ロジスティック回帰分析」を使って統計解析されている!
「あみだくじ」には、「あたり/はずれ」が、中央にあるのか、端にあるのか、知っていさえすれば勝てる!

「あみだくじ」が公平?
本気で言っているんですか?
「あみだくじ」、実は、
横線の存在を、ほぼ無視できるんです。
なので、「あたり/はずれ」が、中央にあるのか、
端にあるのか、
その位置関係さえ知っていれば、
簡単に狙いを的中させてしまえるのです。
信じられませんか?
では、百聞は一見に如かず。
実際に見てみましょう。
例えば、以下のような
「あみだくじ」を行ったとします。
あみだくじルール:
「あみだくじ」で、4人(A君〜D君)の中から1人、罰ゲームを受ける人を決める。
A君のターンからスタート。A君はハズレの位置を決め(図の×印)、紙を折った。他3人(B〜D君)からは「どこにハズレがあるか」分からない状態となった。

ターンは変わり、B~D君たちの番。3人は横線を加え、紙を折った。A君からは「どのように横線が加えられているか」分からない状態となった。
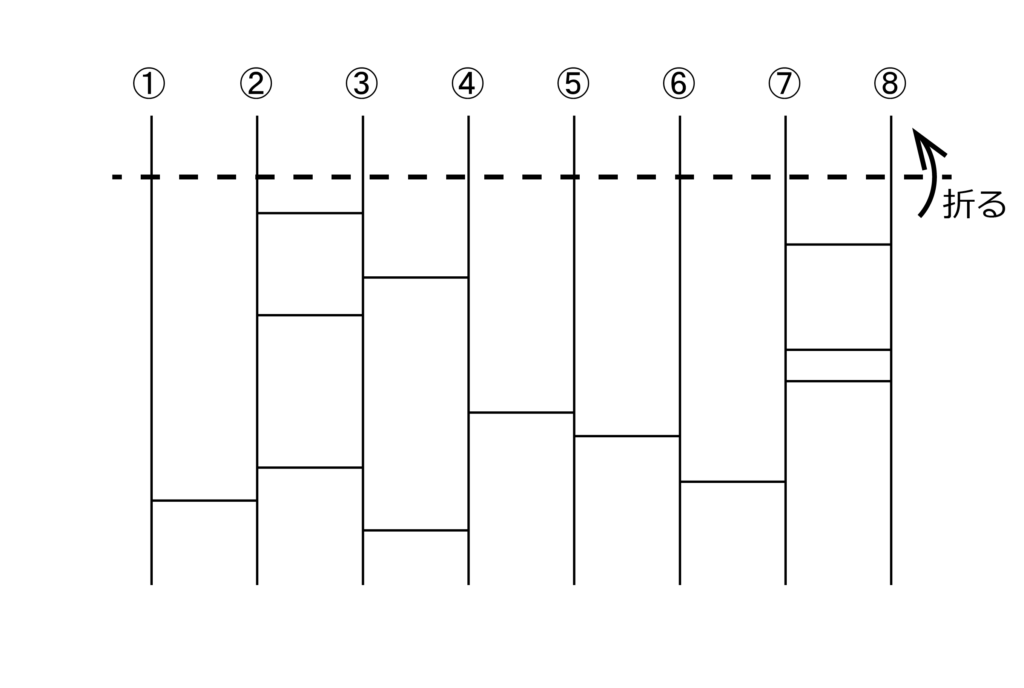
さて、運命の時。まずはテキトーに、1人1つずつ順番に場所を決めていく。そして、全員が1人1つ場所を決めた後、今度は最初とは逆回りの順番で場所を決めていく。結果やいかに…
この「あみだくじ」を、
様々な横線の入れ方をして1000回、
繰り返したシュミレーションが以下となります。
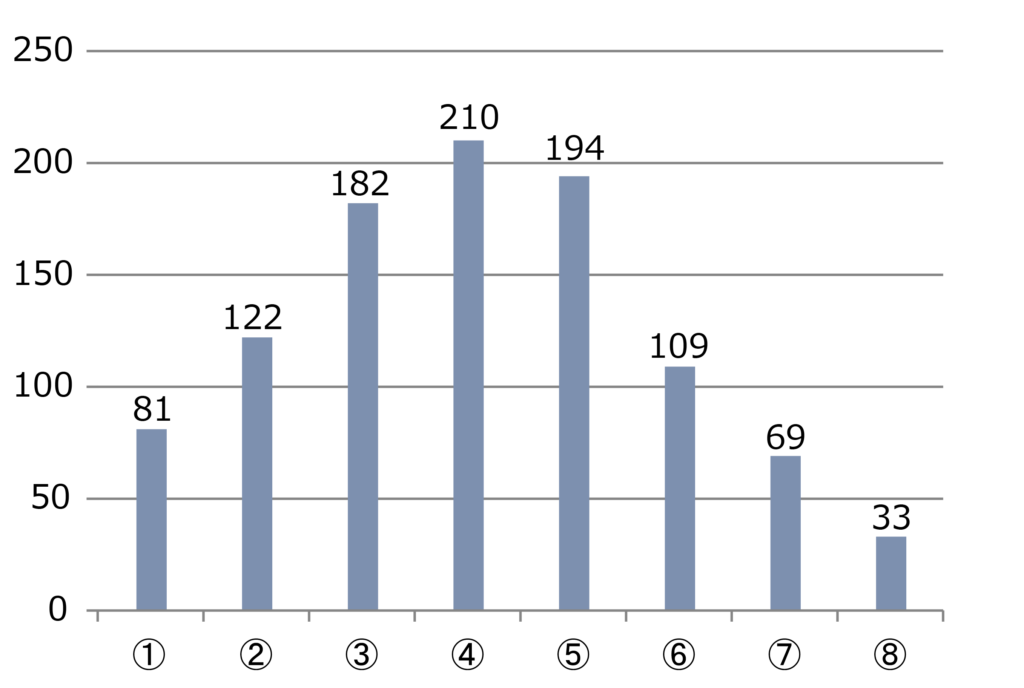
どんな風に横線を加えられようとも、問題なし。
端を選んでおけば、×印を引くことはまずない。
罰ゲームになる可能性は限りなく低いのです。
この事実をA君が知っていたとしたら、
どうでしょうか?
その全数調査、必要ありますか?サンプリング調査でも”妥当な”結果は出せる!

疑問に思ったことが
あるのではないでしょうか?
なんで、サンプリング調査の結果のくせして
あたかも「全数調査をした結果です」みたいに
話しているんだ?と。
例えば、こんな風に。
我がA国の失業率に関する調査結果を報告いたします。
ランダムに国民へアンケート調査をお願いしました(サンプリング調査)。
総数は、全国民の0.5%にあたります。結果、失業率は約0.5%と分かりました。
なんで全国民に調査をお願いしなかったんだ(全数調査)?
…?統計解析を行うので、問題ないと判断しました。
何を言っている!問題だろう。
仮に、その0.5%の国民全員が失業者だった場合は、どうなる?失業率は100%!おかしな結果になる。
我がA国の全人口は1億2000万人。0.5%は60万人だ。考えられなくもない。
それでは、くじ引きで、たとえましょう。
失業率0.5%とは、200個の内、1個しかアタリがないクジ(1÷200=0.005=0.5%)と同じです。
そんな低確率のクジに60万回トライします。これは全国民0.5%、60万人と同じです。
さて、0.5%アタリのゲームに、60万回連勝できるでしょうか?
隕石が今ここに降ってくる心配をしないように、アナタが抱く心配を、私はしませんね。
“確実な”結果は出せないにせよ、
サンプリング調査でも”妥当な”結果は
出せるのです。
予想がつかないなら、さっさと「A/Bテスト」!

「A/Bテスト」を使いこなせるようになれば、
あなたは「キレ者」になれるでしょう。
「A/Bテスト」とは、
「AパターンBパターン両方を
”同条件で”試してみて、比較すること」を
指します。
統計学では「ランダム化比較実験」と
呼ばれているものです。
ストーリーで説明しましょう。
「DM送付は、効果があるのか?」事件:
「このDM送付って本当に意味あるんですかね?」ある日の会議、ポロッと出た意見だった。
この会社では、長年「商品を購入してもらったことのある人」全てにDMを送り続けていたのだ。
「電子メールならまだしも、ウチは紙で送ってる。その費用は、かなりのもの。費用に見合ってるんですかね?」
場は混沌化。これだから、あれだから、あーでもない、こーでもない。様々な意見が飛び交い、誰もが長期戦を覚悟していた。
しかし、突如、会議に終止符が打たれる。一人の男性社員の「ある発案」があったからだ。「A/Bテストで確かめてみましょう。」
男性社員は「テストを行う上での条件」を提示した。
・来月以降、購入してくれた新規客を対象とする
・それらの客を、ランダムに「DMを送る客/送らない客」に分ける
「新規客に絞るのは、比較項目(送る客/送らない客)の条件を揃えるためです。送らない客の中に、古参客が混じってしまうと?DMによる影響を受けていない対称群だったはずなのに、実は過去に送付のDMが影響を与えていました、となってしまう。DM効果の有無が、ぼやけてしまうのです。」
「A/Bテスト」は、この男性がやったように、
条件を揃えることが肝。
もちろん、揃えなくても良い条件もあります。
例えば、今回の場合で言えば、
テストを行う時期。
ボーナスが入る時期と、そうでない時期では、
購買数は、もちろん変わるでしょう。
しかし、同時期に、テストを行なっているため、
ボーナスの影響は無視できます。
ボーナス時期に突入。
再び買ってくれそうな客は増えていますが、
その”同じ環境下で”、「送る客/送らない客」の
比較テストを”同時に”行なっているので問題なし!
という訳です。
年代もありますね。
年金暮らしに入っている層と、
現役会社員の層とでは、
購買意欲は変わるでしょう。
しかし、これは、”ランダムに”
「送る客/送らない客」を選べば、
影響を無視することが出来ます。
たまたま現役層が片方に集中したら、
どうするんだ?
前述のサンプリング調査の説明と同じですよ。
さて、男性が結果を出したようです。
「A/Bテスト」の結果:
・結論、DMを出す価値あり。
・DMを送った客の方が、送らなかった客より再度購入額が高かったと判断できる。
・DMを送った客の再度購入売上額が、DM送付費用を大きく上回った。
この男性、「キレ者」ですね。
一つに絞れないなら、さっさと「A/Bテスト」!

この会社、またDMで揉めているようです。
「どっちのDMが良いんだ!」事件:
DMを、今の時代に合わせ、新デザインに変える方針が決まっていた。方針決定まではスムーズだったが「新デザイン案を、どれにするか」で議論が紛糾してしまった。
「B案にすべきです!」「いいや、A案だね!絶対A!」
「こりゃ長期戦だな」と、誰もが覚悟していた中、「キレ者」の、あの男性が立ち上がった。
「では、A案・B案、どっちも採用しましょう。A・B同時に走らせてみて、出てきた結果を比較するんです。A/Bテストですよ。」
会議でゴチャゴチャ考えるより、
さっさと試しましょう。
いくら話し合っても確実な正解が
出せなさそうなら、さっさと試しましょう。
人件費を浪費して終わりのない会議を
繰り返すより、最終決着をA/Bテストに
任せるのです。
早く、安く、確実な答えを得られますよ。
ほとんどのデータが「重回帰分析」か「ロジスティック回帰分析」を使って統計解析されている!

データ分析って、
何やってるのか訳わかんない意味不明〜
「重回帰分析」と「ロジスティック回帰分析」。
たった2つ。
このたった2つの分析手法の
”簡単なイメージ・ポイント”さえ、
知ってしまえば、”かなり”視界が広がりますよ。
だって、ほとんどのデータが、この
「重回帰分析」か「ロジスティック回帰分析」
を使って解析されているのですから。
| 分析軸(説明変数) | |||||
| 2グループ間の比較 | 多グループ間の比較 | 連続値の多寡で比較 | 複数の要因で同時に比較 | ||
| 比較したいもの(結果変数) | 連続値 | 平均値の違いをt検定 | 平均値の違いを分散分析 | 回帰分析 | 重回帰分析 |
| あり/なし などの二値 | 集計表の記述とカイ二乗検定 | ロジスティック回帰分析 | |||
表はデータ解析手法をまとめたものです。
解析手法、色々ありますね。
でも、大は小を兼ねる。
「t検定」をすべき場面で
「重回帰分析」を行なっても、
「カイ二乗検定」をすべき場面で
「ロジスティック回帰分析」を行なっても、
OKなのです。
こんな背景から、データ解析者は、
この2つの解析手法を多用しています。
「2つだけ知っておけば」と
言った理由、分かりましたか?
それでは、この2つのイメージを
簡単に掴みに行きましょう!
イメージを掴むだけなら「重回帰分析」は、意外と簡単!

中学生の頃の数学で学んだ、
「y=ax+b」覚えていますか?
「重回帰分析」は、このイメージです。
「勉強時間(=x)を増やしたら、
テストの点数(=y)が良くなる」と
言える結果となったかどうか、
そんなy=ax+bのような関係性が
集計したデータから見つかったかどうかを
分析しているだけです。
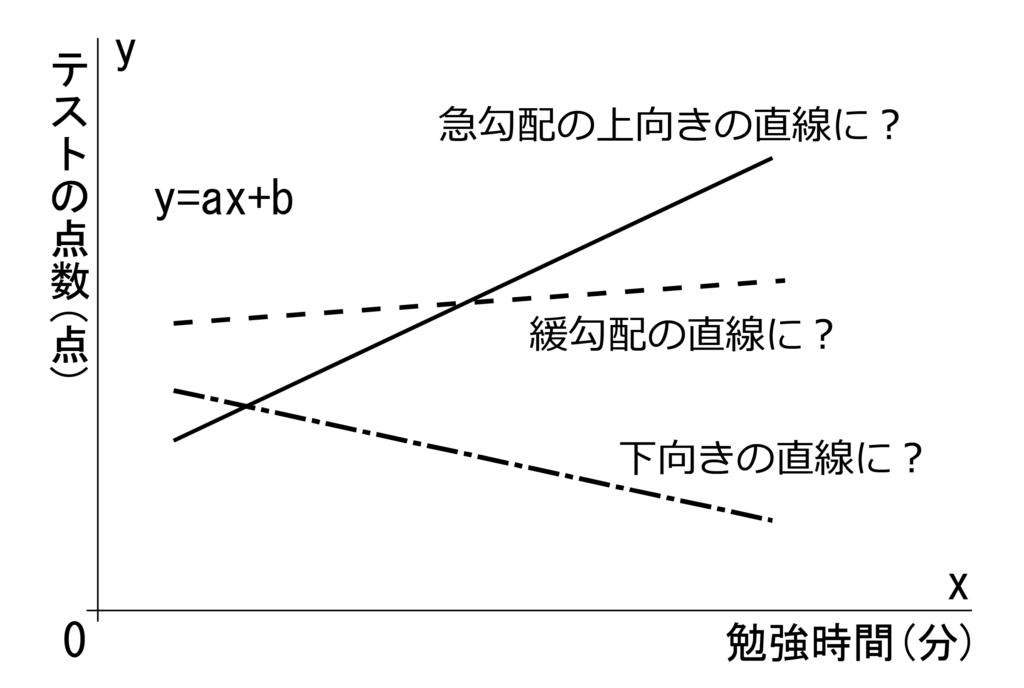
勉強時間がかなりプラスに働いていたのか。
つまり、傾きaが大きい、急勾配の上向き直線の
関係性が確認できる集計結果になったのか。
逆に、地頭などで、勉強時間は関係なし。
傾きaが小さい、緩勾配の直線の関係性が
確認できる集計結果になったのか。
はたまた、勉強嫌いを誘発。
傾きaがマイナス、下向きの直線の関係性が
確認できる集計結果になったのか。
こんな関係性を知ることができるのが、
「重回帰分析」です。
そして、関係するかどうかの項目を
“複数、同時に”解析できるから、
“重”回帰分析という名前なのです。
勉強時間や睡眠時間など、テストの点数に
関係しそうな項目を洗いざらい挙げて、一気に
分析できてしまうのが「重回帰分析」なのです。
さて、では、もう一歩踏み込んでみましょう。
「重回帰分析」の結果の見方も
意外と簡単です。
ある中学数学テストの分析結果を
例に挙げます。
中学生数学テストの正答率への重回帰分析結果
| 回帰係数の推定値 | 標準誤差 | p値 | |
| 「切片」 | 42.33 | ||
| 「男子」である | -1.62 | 1.31 | 0.05以上 |
| 「読み聞かせ」をされたことがある | 3.32 | 1.41 | 0.05未満 |
| 「通塾」している | 16.62 | 1.64 | 0.001未満 |
| 「宿題」を行なっている | 6.29 | 0.92 | 0.001未満 |
| 「勉強時間」の長さ | 0.01 | 0.02 | 0.05以上 |
| 「家・塾での勉強時間がゼロ」である | -5.79 | 2.08 | 0.01未満 |
出所:苅谷剛彦『学力と階層』(朝日新聞出版)
「通塾している/していない」が
かなり関係していたようですね。
推定値16.62とあります。
「通塾している/していない」の要因が、
大体16.62点分の差を生んでいたと言える、
ということです。
大体としたのは、標準誤差1.64とあるからです。
統計処理の関係上、
推定値には、少し幅が生まれてしまいます。
この場合で言えば、
16.62+(1.64×2)点〜16.62-(1.64×2)点となります。
最大16.62+(1.64×2)=18.90点分の差を
生んでいたかもしれないし、
最小16.62-(1.64×2)=13.34点分の差を
生んでいたかもしれない、
と考えて間違いない、ということです。
いずれにせよ、「通塾」は、かなり大きく影響、
つまり「大きい傾きaだった」と言えますね。
さて、かえって勉強時間は
ビミョーな結果だったようです。
なぜならp値0.05以上とあるから。
p値は、そのデータが
「たまたま出た結果かどうか」を示す値です。
サンプリング調査の説明の際、
「たまたま失業者ばかりだったらどうするんだ!」
って話、ありましたよね?
そんな「たまたま」があったかどうかを
教えてくれるのが、この数値です。
慣例的にp値が0.05以上になると
「たまたまだ」と言われています。
勉強時間、関係ないのかもしれませんね。
さて、以上で説明は終わり!
だいぶ視界が広がったのでは、
ないでしょうか?
イメージを掴むだけなら「ロジスティック回帰分析」は、意外と簡単!

「ロジスティック回帰分析」に関しては
結果の見方を少し掴むだけで十分です。
どんな要因が「家庭や塾での勉強時間が
ゼロの生徒」を生み出してしまうのか
調べた結果を例に挙げます。
「家庭や塾での勉強時間がゼロ」の生徒に関する「ロジスティック回帰分析」の結果
| オッズ比の推定値 | p値 | |
| 「男子」である | 0.77 | 0.05~0.10 |
| 「読み聞かせ」をされたことがある | 1.11 | 0.05以上 |
| 「宿題」を行なっている | 0.55 | 0.001未満 |
| 「家庭の文化層が下位」である | 1.78 | 0.01未満 |
| 「家庭の文化層が上位」である | 0.69 | 0.05~0.10 |
| 「父親が大卒」である | 0.60 | 0.01未満 |
出所:苅谷剛彦『学力と階層』(朝日新聞出版)
オッズ比は「約何倍そうなりやすいか」を
示す数値です。
この結果で言えば、文化層下位であると
大体1.78倍、ゼロ生徒を生み出しやすかった
と考えて間違いない、と読み取れるわけです。
約2倍、そうなりやすいと言える。
つまり、「文化層下位かどうか」は、
かなり影響を与える要因だと
判断できるわけです。
ほか、p値は先の「重回帰分析」と同じ。
また、ここでは示していませんが、
ロジスティックにも標準誤差はあります。
もちろん、それが意味するところは
重回帰と同じ。
以上!終わり!
ロジスティックも、かなり簡単でしたよね?
まとめ
以上、
- 「あみだくじ」には、「あたり/はずれ」が、中央にあるのか、端にあるのか、知っていさえすれば勝てる!
- その全数調査、必要ありますか?サンプリング調査でも”妥当な”結果は出せる!
- 予想がつかないなら、さっさと「A/Bテスト」!
- 一つに絞れないなら、さっさと「A/Bテスト」!
- ほとんどのデータが「重回帰分析」か「ロジスティック回帰分析」を使って統計解析されている!
を紹介しました。
本書は、私的最強ビジネス書、
四天王の一人です。
ここまで考え方・見える景色を
好転させてくれる本は
なかなか無いと感じます。
加えて、読みやすい。
「統計」という難しいテーマを
扱っているはずなのに、スラスラ読めます。
専門用語は、ほぼ無し!
簡易な言葉で、やさしく統計リテラシーを
身に付けさせてくれます。
かなりの文量で紹介しましたが、
これでも本書の内容の、ほんの一部。
まだまだ知っておくべきことが
沢山載っています。
ぜひ是非是非!
本書を一度手に取って読んでみてください。
あなたのビジネス人生を
大きく好転させてくれる本だと感じます。
かなり!非常に!めちゃくちゃ!
オススメの本です!
「確かに四天王クラスだ」と
アナタも絶対納得するはずですよ◎
それでは、また!
出典
西内啓 . 統計学が最強の学問である . ダイヤモンド社 , 2013


